БАЛЛИСТИКА , наука о движении под действием некоторых сил тяжелого тела, брошенного в пространство. Баллистика прилагается гл. обр. к исследованию движения артиллерийского снаряда или пули, выпущенных cпомощью того или иного рода метательного оружия. Баллистика прилагается и к исследованию движения бомбы, сброшенной с авиационного аппарата. Для установления законов научной баллистики пользуются методами высшей математики и экспериментом. Баллистика разделяется на внешнюю и внутреннюю.

Внешняя баллистика рассматривает законы движения снаряда в воздухе и других средах, а также законы действия снарядов по различным предметам. Основная задача внешней баллистики заключается в установлении зависимости кривой полета снаряда (траектории) от начальной скорости v 0 , угла бросания ϕ, калибра 2R, веса Р и формы снаряда, а также и от всякого рода обстоятельств, сопровождающих стрельбу (например, метеорологических). Первые исследования в области внешней баллистики принадлежат Тарталья (1546 г.). Галилей установил, что траекторией тела, брошенного в безвоздушном пространстве, является парабола (фиг. 1).

Уравнение этой параболы таково:

Траектория симметрична относительно вершины А, так что Аа является осью параболы; угол падения ϴ с равен углу бросания ϕ; скорость v с в точке падения С равна начальной скорости v 0 ; наименьшей скоростью снаряд обладает в вершине А; времена полета по восходящей и нисходящей ветвям равны.

Дальность полета X в безвоздушном пространстве определяется из выражения

которое указывает, что наибольшая дальность получается при угле бросания ϕ = 45°. Полное время полета Т в безвоздушном пространстве находится из выражения

Ньютон в 1687 г. показал, что траектория тела, брошенного в воздухе, не есть парабола, и на основании ряда опытов пришел к заключению, что сила сопротивления воздуха пропорциональна квадрату скорости движения тела. Эйлер, Лежандр и другие также принимали ее пропорциональной квадрату скорости. Аналитическое выражение силы сопротивления воздуха выводилось как теоретически, так и на основании опытных данных. Первая систематическая работа по этому вопросу принадлежит Робинсу (1742 г.), исследовавшему сопротивление воздуха движению сферических пуль. В 1839-1840 гг. Пиобер, Морен и Дидион в Меце произвели такого же рода опыты над сферическими снарядами. Введение нарезного оружия и продолговатых снарядов послужило сильным толчком для изучения законов сопротивления воздуха полету снаряда. В результате опытов Башфорта в Англии (1865-1880 гг.) над продолговатыми и над сферическими снарядами, на основании работ Маиевского в России (1868-1869 гг.), завода Круппа в Германии (1881-1890 гг.) и Хожеля в Голландии (1884 г.) оказалось возможным выразить силу сопротивления воздуха ϱ таким одночленом:

где λ - коэффициент, зависящий от формы снаряда, А - численный коэффициент, π - отношение длины окружности к диаметру, R - радиус цилиндрической части снаряда, П - плотность воздуха при стрельбе и П 0 = 1,206 кг - плотность воздуха при 15°, давлении атмосферы в 750 мм и влажности 50%. Коэффициент А и показатель n определяются из опыта и различны для разных скоростей, а именно:

Общие свойства траектории невращающегося снаряда в воздухе устанавливаются на основании дифференциальных уравнений движения его центра тяжести в вертикальной плоскости стрельбы. Эти уравнения имеют вид:

В них: ϱ - сила сопротивления воздуха, Р - вес снаряда, ϴ - угол наклона касательной в данной точке траекторий к горизонту, v - скорость снаряда в данной точке, v 1 = v∙cos ϴ - горизонтальная проекция скорости, s - длина дуги траектории, t - время, g- ускорение силы тяжести. На основании этих уравнений С.-Робер указал такие главные свойства траектории: она выгнута выше горизонта, вершина ее находится ближе к точке падения, угол падения больше угла бросания, горизонтальная проекция скорости постепенно убывает, наименьшая скорость и наибольшая кривизна траектории находятся за вершиной, нисходящая ветвь траектории имеет асимптоту. Профессором Н. Забудским, кроме того, добавлено, что время полета в нисходящей ветви больше, чем в восходящей. Траектория снаряда в воздухе изображена на фиг. 2.

При движении снаряда в воздухе угол наибольшей дальности вообще меньше 45°, но м. б. случаи, когда этот угол больше 45°. Дифференциальные уравнения движения центра тяжести снаряда не интегрируются, и поэтому основная задача внешней баллистики в общем случае не имеет точного решения. Довольно удобный способ приближенного решения был дан впервые Дидионом. В 1880 Сиаччи предложил удобный для практики способ решения задачи прицельной стрельбы (т. е. когда ϕ ≤ 15°), применяемый и доныне. Для удобства вычислений Сиаччи составлены соответствующие таблицы. Для решения задач навесной стрельбы (т. е. при ϕ > 15°), когда начальная скорость меньше 240 м/сек, дан способ и составлены необходимые таблицы Отто, измененные впоследствии Сиаччи и Лордильоном. Башфорт также дает способ и таблицы для решения задач навесной стрельбы при скоростях свыше 240 м/сек. Профессор Н. Забудский для решения задач навесной стрельбы при начальных скоростях от 240 до 650 м/сек принимает силу сопротивления воздуха пропорциональной 4-й степени скорости и дает способ решения при этом допущении. При начальных скоростях, превосходящих 650 м/сек, для решения задач навесной стрельбы приходится разбивать траекторию на три части, причем крайние части вычислять по способу Сиаччи, а среднюю - по способу Забудского. За последние годы получил широкое распространение и общее признание способ решения основной задачи внешней баллистики, основанный на методе Штермера - численного интегрирования дифференциальных уравнений. Применение этого метода к решению задач баллистики было впервые произведено академиком А. Н. Крыловым. Метод численного интегрирования является универсальным, т. к. пригоден для любых скоростей и углов бросания. При этом способе легко и с большой точностью м. б. учтено изменение плотности воздуха с высотой. Это последнее имеет большое значение при стрельбе под большими углами бросания, до 90°, со значительными начальными скоростями, порядка 800-1000 м/сек (стрельба по воздушным целям), и особенно при так называемой сверхдальней стрельбе, т. е. на дистанцию 100 и более км.

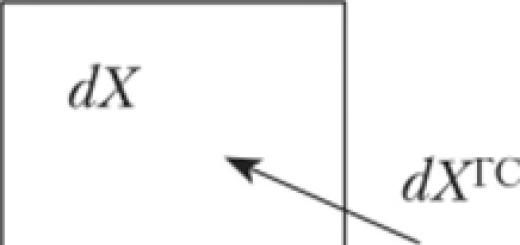
Основанием для решения вопроса о стрельбе на такие дистанции служит следующая идея. Снаряд, выпущенный с очень большой начальной скоростью, например, 1500 м/сек, под углом бросания 50-55°, быстро долетает в восходящей ветви своей траектории до таких слоев атмосферы, в которых плотность воздуха чрезвычайно мала. Считают, что на высоте 20 км плотность воздуха в 15 раз, а на высоте 40 км в 350 раз меньше плотности воздуха на поверхности земли; вследствие этого в такое же соответственно количество раз на этих высотах уменьшается и сила сопротивления воздуха. Т. о. можно считать часть траектории, проходящую в слоях атмосферы, лежащих выше 20 км, параболой. Если же касательная к траектории на высоте 20 км будет иметь наклон к горизонту в 45°, то дальность по безвоздушному пространству будет наибольшей. Чтобы обеспечить угол в 45° на высоте 20 км, нужно снаряд бросить с земли под углом, большим 45°, т. е. под углом в 50-55°, в зависимости от начальной скорости, калибра и веса снаряда. Например, (фиг. 3): снаряд, брошен, под углом к горизонту в 55° с начальной скоростью в 1500 м/сек; в точке а восходящей ветви его скорость стала равна 1000 м/сек, а касательная к траектории в этой точке составляет с горизонтом угол в 45°.

При этих условиях дальность полета а b по безвоздушному пространству будет составлять:

а дальность по горизонту точки стояния орудия ОС будет более 102 км на сумму участков ОА и ВС, вычисление величины которых удобнее и точнее всего можно произвести способом численного интегрирования. При точном расчете сверхдальней траектории приходится принимать во внимание влияние вращения земли, а для траекторий с дальностью в несколько сот км (теоретически возможный случай) также шарообразную форму земли и изменение ускорения силы тяжести как по величине, так и по направлению.

Первые существенные теоретические исследования движения продолговатого снаряда, вращающегося около своей оси, были произведены в 1859 г. С.-Робером, мемуары которого послужили основой для работ по этому вопросу Маиевского в России. Аналитические исследования привели Маиевского к заключению, что ось фигуры снаряда, когда поступательная скорость не слишком мала, имеет колебательное движение вокруг касательной к траектории, и позволили изучить это движение для случая прицельной стрельбы. Де-Спарре удалось привести эту задачу к квадратурам, а профессору Н. Забудскому - распространить вывод де-Спарре на случай навесной стрельбы. Дифференциальные уравнения вращательного движения снаряда при принятии некоторых практически возможных допущений имеют вид:

здесь: δ - угол между касательной к траектории и осью фигуры снаряда; v - угол между вертикальной плоскостью, проходящей через ось канала орудия, и плоскостью, проходящей через касательную к траектории и ось фигуры снаряда; k- момент силы сопротивления воздуха относительно центра тяжести снаряда; А - момент инерции снаряда относительно оси; р 0 - проекция угловой скорости вращения снаряда на его ось; ϴ - угол наклона касательной в данной точке траектории к горизонту; t - время.

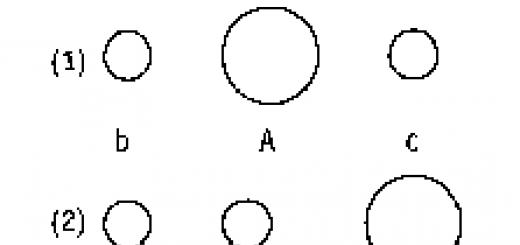
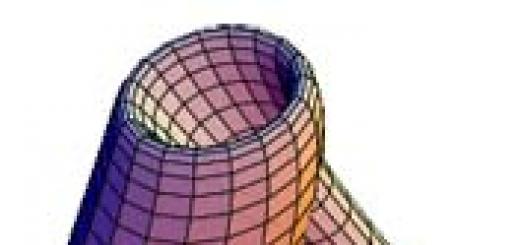
Эти уравнения точно не интегрируются. Исследование вращательного движения продолговатого снаряда приводит к следующему основному выводу: при прицельной стрельбе ось снаряда всегда отклонена в одну сторону от плоскости стрельбы, а именно - в сторону вращения снаряда, если смотреть на него сзади; при навесной стрельбе это отклонение может быть и в обратную сторону. Если представить себе плоскость, всегда остающуюся перпендикулярной к касательной к траектории и отстоящую во время полета снаряда всегда на одном и том же расстоянии от его центра тяжести, то ось фигуры снаряда вычертит на этой плоскости сложную кривую вида, показанного на фиг. 4.

Большие петли этой кривой являются результатом колебательного движения оси фигуры снаряда вокруг касательной к траектории, это - т. н. прецессия ; малые же петли и волнистость кривой есть результат несовпадения мгновенной оси вращения снаряда с осью его фигуры, это - так наз. нутация . Для получения большей меткости снаряда необходимо добиваться уменьшения нутации. Отклонение снаряда от плоскости стрельбы вследствие отклонения его оси называется деривацией . Маиевским выведена простая формула для величины деривации при прицельной стрельбе; эта же формула м. б. применена и при навесной стрельбе. Вследствие деривации проекция траектории на горизонт, плоскость получает вид, указанный на фиг. 5.

Т. о. траектория вращающегося снаряда является кривой двоякой кривизны. Для правильного полета продолговатого снаряда ему необходимо придать соответствующую скорость вращения вокруг оси. Профессор Н. Забудский дает выражение минимальной скорости вращения, необходимой для устойчивости снаряда на полете в зависимости от его конструктивных данных. Вопросы вращательного движения снаряда и влияния этого движения на полет его крайне сложны и мало изучены. Лишь за последние годы предпринят ряд серьезных исследований этого вопроса гл. обр. во Франции, а также и в Америке.

Изучение действия снарядов по различным предметам ведется внешней баллистикой гл. обр. путем опытов. На основании опытов Мецкой комиссии даны формулы для вычисления величин углублений снарядов в твердые среды. Опыты Гаврской комиссии дали материал для вывода формул пробивания брони. Испанский артиллерист де-ла-Лав на основании опыта дал формулы для вычисления объема воронки, образующейся при разрыве снаряда в грунте; объем этот пропорционален весу разрывного заряда и зависит от скорости падения снаряда, его формы, качества грунта и свойств взрывчатого вещества. Способы решения задач внешней баллистики служат основанием для составления таблиц стрельбы. Вычисление табличных данных производится после определения стрельбой на 2-3 дистанции некоторых коэффициентов, характеризующих снаряд и орудие.

Внутренняя баллистика рассматривает законы движения снаряда в канале орудия под действием пороховых газов. Только зная эти законы, можно проектировать орудие требуемой мощности. Т. о. основная задача внутренней баллистики заключается в установлении функциональной зависимости давления пороховых газов и скорости движения снаряда в канале от проходимого им пути. Для установления этой зависимости внутренняя баллистика пользуется законами термодинамики, термохимии и кинетической теории газов. С.-Робер первый воспользовался началами термодинамики при изучении вопросов внутренней баллистики; затем французский инженер Сарро дал ряд капитальных трудов (1873-1883 гг.) по вопросам внутренней баллистики, послуживших основой для дальнейших работ различных ученых, и этим положил начало современному рациональному изучению вопроса. Явления, происходящие в канале данного орудия, существенным образом зависят от состава пороха, формы и размеров его зерен. Продолжительность горения порохового зерна зависит, главным образом, от его наименьшего размера – толщины - и скорости горения пороха, т. е. быстроты проникания пламени в толщу зерна. Скорость горения прежде всего зависит от давления, под которым оно происходит, а также и от природы пороха. Невозможность точного изучения горения пороха заставляет прибегать к опытам, гипотезам и допущениям, упрощающим решение общей задачи. Сарро выразил скорость горения и пороха такой функцией давления

где А - скорость горения при давлении в 1 кг/см 2 , a v - показатель, зависящий от сорта пороха; v, вообще говоря, меньше единицы, но очень близка к ней, поэтому Себер и Гюгоньо упростили формулу Сарро, приняв v = 1. При горении под переменным давлением, что имеет место в канале орудия, скорость горения пороха является также величиной переменной. Согласно работ Вьеля можно считать, что бездымные пороха горят концентрическими слоями, горение же дымных порохов такому закону не подчиняется и происходит весьма неправильно. Закон развития давлений пороховых газов в закрытых сосудах установлен Ноблем в таком виде:

P 0 - давление атмосферы; w 0 - объем продуктов разложения 1 кг пороха при 0° и давлении 760 мм, считая воду газообразной; Т 1 - абсолютная температура разложения пороха; W - объем сосуда, в котором происходит сгорание; w- вес заряда; α - коволюм, т. е. объем продуктов разложения 1 кг пороха при бесконечно большом давлении (вообще принимают α = 0,001w 0); Δ - плотность заряжания, равная при метрических мерах w/W; f = RT 1 - сила пороха, измеряемая в единицах работы на единицу веса заряда. Для упрощения решения общей задачи о движении снаряда в канале орудия предполагают: 1) что воспламенение всего заряда происходит одновременно, 2) что скорость горения пороха в течение всего процесса пропорциональна давлению, 3) что горение зерен происходит концентрическими слоями, 4) что количество теплоты, отделяемое каждой равной долей заряда, объемы и состав газов, а также сила пороха постоянны во все время горения заряда, 5) что нет передачи теплоты стенкам орудия и снаряду, 6) что нет никаких потерь газов и 7) что нет волнообразного движения продуктов взрыва. Принимая эти основные допущения и еще некоторые, различные авторы дают решение основной задачи внутренней баллистики в виде той или иной системы дифференциальных уравнений движения снаряда. Интегрировать в общем виде эти уравнения не представляется возможным, а потому прибегают к приближенным методам решения. В основе всех этих методов лежит классическое решение задачи внутренней баллистики, предложенное Сарро и заключающееся в интегрировании дифференциальных уравнений движения снаряда с помощью замены переменных. После классических формул Сарро наиболее известными являются формулы, предложенные Шарбонье и Сюго.

Баллистики Бианки (Италия), Кранц (Германия) и Дроздов (Россия) также дают свои методы решения основной задачи. Все вышеуказанные методы представляют значительные трудности для практического применения вследствие их сложности и необходимости таблиц для вычисления различного рода вспомогательных функций. Методом численного интегрирования дифференциальных уравнений задача внутренней баллистики также м. б. решена. Для практических целей некоторыми авторами даются эмпирические зависимости, пользуясь которыми можно достаточно точно решать задачи внутренней баллистики. Наиболее удовлетворительными из таких зависимостей являются формулы Гейденрейха, ле-Дюка, Оккинггауза (Oekkinghaus) и дифференциальные формулы Киснемского. Закон развития давления и закон скоростей движения снаряда в канале орудия графически представлены на фиг. 6.

Подробное рассмотрение вопроса о влиянии формы и размеров порохового зерна на развитие давлений в канале орудия приводит к выводу, что возможно такое зерно, при котором давление, достигнув некоторой величины, не будет убывать по мере движения снаряда в канале, а останется таким вплоть до полного сгорания заряда. Такой порох будет обладать, как говорят, полной прогрессивностью. С помощью такого пороха снаряд получит наибольшую начальную скорость при давлении, не превосходящем предварительно заданное.

Изучение вращательного движения снаряда в канале под действием нарезов имеет конечной целью определение усилий, действующих на ведущие части, что нужно для расчета их прочности. Давление в данный момент на боевую грань нареза или выступа ведущего пояска

где λ - коэффициент, зависящий от снаряда, находится в пределах 0,55-0,60 для принятых конструкций снарядов; n- число нарезов; Р - давление газов; s - площадь поперечного сечения канала; α - угол наклона нарезов к производящей канала; m - масса снаряда; v - скорость снаряда; у = f(x) - уравнение кривой нарезки, развернутой на плоскость (для нарезки постоянной крутизны)

Наиболее распространенным типом нарезки является постоянная, представляющая собой при разворачивании на плоскость прямую линию. Крутизна нарезки определяется скоростью вращений снаряда вокруг оси, необходимой для устойчивости его на полете. Живая сила вращательного движения снаряда составляет около 1% живой силы его поступательного движения. Кроме сообщения снаряду поступательного и вращательного движений, энергия пороховых газов тратится на преодоление сопротивления ведущего пояска снаряда врезанию в нарезы, трения на боевых гранях, трения продуктов горения пороха, атмосферного давления, сопротивления воздуха, веса снаряда и на работу растяжения стенок ствола. Все эти обстоятельства м. б. в той или иной степени учтены или теоретическими соображениями, или на основании опытного материала. Потеря газами теплоты на нагрев стенок ствола зависит от условий стрельбы, калибра, температуры, теплопроводности и т. п. Теоретические соображения по этому вопросу весьма затруднительны, непосредственных же опытов относительно этой потери не производилось; так обр. этот вопрос остается открытым. Развивающиеся в канале ствола при выстреле чрезвычайно высокие давления (до 3000-4000 кг/см 2) и температуры оказывают разрушительное влияние на стенки канала - происходит т. н. выгорание его. Существует несколько гипотез, объясняющих явление выгорания, из них главнейшие принадлежат профессору Д. Чернову, Вьелю и Шарбонье.

Теория

Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения ; проекции ускорения на координатные оси равны а х = 0, а у = -g.

Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

,

где – начальная скорость, α – угол бросания.

Координаты тела, следовательно, изменяются так:

При нашем выборе начала координат начальные координаты (рис. 1) Тогда

Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.

Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t 0 . Подставляя значение (2) в первую формулу (1), получаем:

.

(3)

Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.

Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем

Горбанева Лариса Валерьевна

Баллистическое движение

Баллистическое движение – движение тела в пространстве под действием внешних сил.

Рассмотрим движение тел под действием силы тяжести. Самый простой случай движения тел под действием силы тяжести – свободное падение с начальной скоростью, равной нулю. В этом случае тело движется прямолинейно с ускорением свободного падения по направлению к центру Земли. Если начальная скорость тела отлична от нуля и вектор начальной скорости направлен не по вертикали, то тело под действием силы тяжести движется с ускорением свободного падения по криволинейной траектории (параболе).

Пусть тело брошено под углом а к горизонту с начальной скоростью V 0 .

Исследуем это движение, то есть определим траекторию движения, время полета, дальность полета, максимальную высоту, на которую поднимется тело, скорость тела.

Запишем уравнения движения для координат х, у тела в любой момент времени и для проекций его скорости на оси X и Y:

,

,

Выберем систему координат так, как показано на рисунке. При этом , .

На тело действует только сила тяжести, значит, оно движется с ускорением только вдоль оси Y ( .

Вдоль оси X тело движется равномерно ( с постоянной скоростью .

Проекции начальной скорости на оси Х и Y :

, .

Тогда уравнения движения тела примут вид:

,

Проекции скорости на оси X и Y в любой момент времени:

,

Чтобы найти траекторию движения надо найти аналитическое уравнение кривой, по которой движется тело в пространстве. Для этого надо решить систему уравнений:

Выразим из второго уравнения и подставим в первое уравнение. В результате получим: . Это уравнение второго порядка описывает параболу, ветви которой направлены вниз, центр параболы смещен относительно начала координат.

Чтобы определить время полета тела воспользуемся уравнением для определения y: . Согласно выбранной нами системы координат y=0 соответствует началу и окончанию движения тела. Тогда можно записать: или .

У этого уравнения два корня: . Действительно, как и определено ранее, на земле тело окажется дважды в начале и в конце пути. Тогда время полета определяет второй корень: .

Зная время полета легко определить дальность полета, то есть максимальную координату x max:

Максимальная координата y max определяет максимальную высоту подъема тела. Для того чтобы ее найти надо в уравнение подставить время подъема t под, которое определяется из условия, что в наивысшей точке подъема равна 0:

Тогда .

Таким образом, .

Проекция скорости на ось Х: – остается неизменной, а проекция скорости на ось Y изменяется следующим образом: . Для определения скорости на любой высоте h необходимо знать время, когда тело будет находиться на этой высоте h – t h . Это время можно найти из уравнения

Время имеет два значения так как на высоте h тело будет находиться дважды, в первый раз – двигаясь вверх, второй раз двигаясь вниз. Поэтому скорость тела на высоте h определится формулами:

В первой точке .

Во второй точке

Модуль скорости на любой высоте определяется по формуле

Можно найти тангенс угла наклона скорости к оси X:

Большинство задач на баллистическое движение является частным случаем или вариацией этой общей задачи.

Пример 1. Под каким углом к горизонту надо бросить тело, чтобы высота его подъема была равна дальности полета?

Высоту подъема тела определим по формуле , дальность полета .

По условию задачи H max =S , поэтому

Решая это уравнение получим tgα=4.

Пример 2. Тело брошено под углом α=π/6 рад к горизонту из положения с координатой y 0 =5м над поверхностью Земли. Начальная скорость тела равна 10м/с. Определить координату y max наивысшей точки подъема тела над поверхностью Земли, координату x п точки падения тела на поверхность Земли и скорость V п в этой точке.

Р
ешение:

Выбрав систему координат, как показано на рисунке.

Координата наивысшей точки траектории тела в выбранной системе координат определяется формулой: или .

=6,3м

Для определения координаты точки падения x п необходимо найти время движения тела до точки приземлении. Время t п определим из условия y п =0: .

Решая данное уравнение получаем: .

Подставив значение величин, получаем:

=1,6с.

Второй корень не имеет физического смысла.

Тогда подставив значение величины t п в формулу

Найдем .

Конечная скорость тела

Угол между осью OX и вектором V п

Пример 3. Артиллерийское орудие расположено на горе высотой h. Снаряд вылетает из ствола со скоростью V 0 ,направленной под углом α к горизонту. Пренебрегая сопротивлением воздуха, определите: а) дальность полета снаряда по горизонтальному направлению, б) скорость снаряда в момент падения, в) угол падения, г) начальный угол стрельбы, при котором дальность полета наибольшая.

Решение. Для решения задачи сделаем чертеж, при этом систему координат выбираем так, чтобы ее начало совпало с точкой бросания, а оси были направлены вдоль поверхности Земли и по нормали к ней в сторону начального смещения снаряда.

Запишем уравнения движения и скорости снаряда в проекциях на оси Х и Y:

В момент времени t 1 , когда снаряд упадет на землю, его координаты равны: x=S, y= – h .

Результирующая скорость в момент падения равна: .

Для определения скорости снаряда в момент падения V и дальности полета S найдем время из уравнения учитывая y= – h .

Решением этого уравнения: .

Подставляя выражение для t 1 в формулы для определения координаты x с учетом x=S , соответственно получаем:

.

Чтобы найти V надо знать V x и V y .

Как было определено ранее .

Для определения V y подставим в формулу значение t 1 и получаем: .

Из полученных результатов можно сделать следующие выводы.

Если h=0, т.е. снаряды падают на уровне вылета, и, произведя преобразования формулы , получаем дальность полета .

Если при этом угол бросания равен 45° (sin 2α=1), то при заданной начальной скорости V 0 дальность полета наибольшая: .

Подставив в выражение для определения скорости значение h=0, получим, что скорость снаряда в момент его подлета к уровню, с которого был произведен выстрел, равна его начальной скорости: V=V 0 .

При отсутствии сопротивления воздуха скорость падения тел равна по модулю их начальной скорости бросания независимо от того, под каким углом было брошено тело, лишь бы точки бросания и падения находились на одном уровне. Учитывая, что проекция скорости на горизонтальную ось с течением времени не изменяется, легко установить, что в момент падения скорость тела образует с горизонтом такой же угол, как и в момент бросания.
Подставляя выражение для S=S max в формулу для определения угла бросания, получим для угла α, при котором дальность полета наибольшая: .

Задачи для самостоятельного решения .

Ф.9.1. Тело брошено горизонтально со скоростью 20м/с. Определить смещение тела от точки бросания, ΔS, при котором скорость будет направлена под углом 45° к горизонту.

Ф.9.2. Под каким углом α надо бросить тело, чтобы дальность полета была наибольшей.

Ф.9.3. Самолет летит горизонтально со скоростью 360км/ч на высоте 490м. Когда он пролетает над точкой А, с него сбрасывают пакет. На каком расстоянии от точки А пакет упадет на землю?

Ф.9.4. Тело свободно падает с высоты 4м. На высоте 2м оно упруго ударяется о небольшую закрепленную площадку под углом 30° к горизонту. Найти полное время движения тела и дальность его полета.

Ф.9.5. Необходимо с земли попасть камнем в цель с расстояния S. Цель расположена на высоте h. При какой наименьшей начальной скорости камня можно это сделать?

Ф.9.6. Из точки с координатами x 0 , y 0 брошено тело под углом α 0 к горизонту с начальной скоростью V 0 (см. рисунок). Найти: положение и скорость тела через время t, уравнение траектории полета тела, полное время полета, наибольшую высоту подъема, угол, под которвм надо бросить тело, чтобы высота его подъема была равна дальности полета (при условии, что x 0 =y 0 =0 ).

Ф.9.7. С вышки высотой 20м из пистолета под углом 30° к горизонту произведен выстрел. Определить скорость вылета, высоту подъема и дальность полета пули, если при падении она прошла последние 20м пути (высоту вышки) за 0,5с. Сопротивлением воздуха пренебречь.

Ф
.9.8. Камень брошен на склоне горы под углом α к ее поверхности (см. рис.). Определите дальность полета камня и его наибольшую высоту подъема над склоном, если начальная скорость камня V 0 , угол наклона горы к горизонту β. Сопротивление воздуха не учитывать.

Ф.9.9. Тело брошено со стола горизонтально. При падении на пол его скорость равна 7,8м/с. Высота стола H=1,5м. Чему равна начальная скорость тела?

Ф.9.10. Камень брошен под углом α 0 =30° к горизонту со скоростью V 0 =10м/с. Через какое время камень будет на высоте 1м?

Ф.9.11. Два тела брошены под углами α 1 и α 2 к горизонту из одной точки. Каково отношение сообщенных им скоростей, если они упали на землю в одном и том же месте?

Ф.9.12. Тело брошено горизонтально со скоростью 20м/с. Определить смещение тела от точки бросания при котором скорость будет направлена под углом 45° к горизонту.

В разделе на вопрос Физика. Баллистическое движение. Помогите найти Начальную скорость. заданный автором Eldar Nezametdinov лучший ответ это Если альфа - угол с линией горизонта, т. е. напрвлением ОХ, то Uо надо разложить на вертикальную (вдоль оси ОY и горизонтальную составляющие, т. е Uoy=Uo Sin(alfa) и Uox= UoCos(alfa)
Изменение скорости вдоль оси OY в скалярном выражении при движении вверх (т. е. направление вектором скорости и ускорения мы уже учли)
Uy=Uoy -gt=Uo Sin alfa - gt/2 =0, где t- время всего полета
Т. е. Uo=(gt)/(2 Sin(alfa))=(10х2)/(2х0.5)=20 (м/c)
Eldar Nezametdinov
Мыслитель
(5046)
откуда двойка взялась?
Дело такое
Uy = Uosina - gT*T/2
у вас написано
Uy = Uosina - gT/2
я вот не пойму) как вы так отделались от Т*Т сделали Т....причем равную 2ке)

Ответ от 22 ответа [гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Физика. Баллистическое движение. Помогите найти Начальную скорость.

Ответ от Леонид Фурсов [гуру]
решение. x(t)=v0*(cos(a))*t; y(t)=v0*(sin(a))*t-0,5*g*t^2; vy=v0*(sin(a))-g*t;
1. vy=0 (условие для нахождения максимальной высоты подъема. Сначала находите время подъема, потом подставляете в формулу y(t)=v0*(sin(a))*t-0,5*g*t^2 и находите максимальную высоту подъема) .
2. y(t)=0 -условие для нахождения длительности полета, а по нему и дальности полета.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Подобные документы

История возникновения баллистического движения. Баллистика как наука. История открытия закона всемирного тяготения. Применение баллистики на практике. Траектория полета снаряда, баллистической ракеты. Перегрузки, испытываемые космонавтами в невесомости.

реферат , добавлен 27.05.2010


Движение, возникающее при отделении от тела со скоростью какой-либо его части. Использование реактивного движения моллюсками. Применение реактивного движения в технике. Основа движения ракеты. Закон сохранения импульса. Устройство многоступенчатой ракеты.

реферат , добавлен 02.12.2010


Характеристика движения объекта в пространстве. Анализ естественного, векторного и координатного способов задания движения точки. Закон движения точки по траектории. Годограф скорости. Определение уравнения движения и траектории точки колеса электровоза.

презентация , добавлен 08.12.2013


Построение траектории движения тела, отметив на ней положение точки М в начальный и заданный момент времени. Расчет радиуса кривизны траектории. Определение угловых скоростей всех колес механизма и линейных скоростей точек соприкосновения колес.

контрольная работа , добавлен 21.05.2015


Принципы реактивного движения, которые находят широкое практическое применение в авиации и космонавтике. Первый проект пилотируемой ракеты с пороховым двигателем известного революционера Кибальчича. Устройство ракеты-носителя. Запуск первого спутника.

презентация , добавлен 23.01.2015


Кинематика, динамика, статика, законы сохранения. Механическое движение, основная задача механики. Материальная точка. Положение тела в пространстве - координаты. Тело и система отсчета. Относительность механического движения. Состояние покоя, движения.

презентация , добавлен 20.09.2008


Составление расчетной схемы установки. Нахождение уравнения траектории движения точки. Построение траектории движения в соответствующих координатах и участка ее в интервале времени. Линейные скорости звеньев и передаточные числа зубчатых зацеплений.

задача , добавлен 27.12.2010


Закон движения груза для сил тяжести и сопротивления. Определение скорости и ускорения, траектории точки по заданным уравнениям ее движения. Координатные проекции моментов сил и дифференциальные уравнения движения и реакции механизма шарового шарнира.

контрольная работа , добавлен 23.11.2009